GREGORY'S TRANSFORMATION
|
ROLLING CURVES |

|
| Progressive drawing of cardioid-deltoid traced by a variable circle in a nephroid and 2-hypocycloid (diameter) | Half circle wheel rolling in a rectangle |
 |
-2Variablecircles.gif) |
 |
| Two ortho-cycloidals translating inside two cycloid-envelopes | Ortho-cycloidals : Nephroid/Astroid turning inside a couple of 3-epi-cycloid and deltoid | Euler Serret rolling curve |
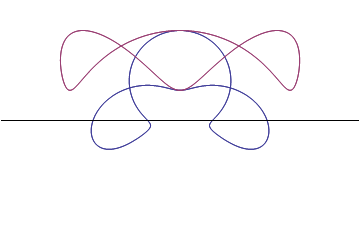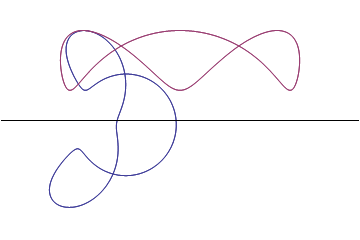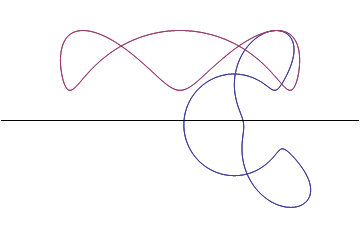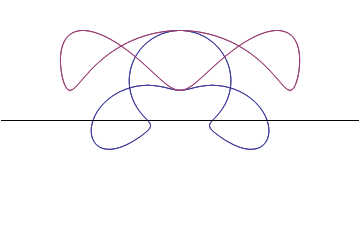 |
 |
 |
| Pole outside the wheel | Tschirnhausen's cubic rolling base line envelope is an equal TC | Wheel for a cardioid ground and its axis |
Some papers about generalized wheels and grounds : |
|||
| Document | Abstract | Document | Abstract |
|---|---|---|---|
|
The wheel is not round (in french) |
(1983) The wheel, this old invention, can be seen as the most simple case of a wide generalisation as shown by "Al-Tusi/Cardan rolling circles" and "Gregoire de St Vincent/torricelli Archimede spiral wheel and parabola" example. James Gregory found a transformation which gives - in simple formulas with only one quadrature - the couple of curves that roll one on the other so that the pole runs along a line. We give many classic and new examples. | The generalized wheel | (1988) We recall the Gregory's transformation and its geometric elementary properties, the theorem of Steiner-Habich and some links with curves rolling one on the other about two fixed poles. We show that they can roll on a common ground in such a way that the poles run along two parallel lines in the plane. |
Some papers about geometry of curves generalized wheels ortho-cycloidals: |
|||
| Document | Abstract | Document | Abstract |
|
Some plane curves (Part XXIX) New !
|
From the classes of curves Ck(n, p), generalizations of sinusoidal spirals, we extract some special series of curves with explicit polar equation ρ = f(θ) . Curves in C1(n, p), C2(n, p), C3(n, p) have simple parametric equation with a natural parameter u linked to polar angle θ by a linear relation : V = u, V = π/2 − 2u and V = 3u. |
The Quintic of l'Hopital (Part XXX) New !
|
We present some properties of the Quintic of l'Hopital found by the marquis de l'Hopital in 1700 as a special solution of a mechanical problem posed by Johann Bernoulli in 1696. This curve has similarities with the Tschirnhausen's Cubic. |
|
Some plane curves (Part XXVII) |
Some plane curves are presented with various properties using elementary geometry, pedals, Mc Laurin and Gregory (GT /GT −1) transformations. |
Some special roulettes and envelopes (Part XXVIII) |
Some examples of general roulettes and envelopes of lines in the plane are presented specially by rolling curves as wheels adapted to a circular ground. We use classes of curves in C1(n, p), C2∗(n, p) to exploit the simple lineary relation between θ and V that facilitates the calculations. |
|
Caustics by reflection and curves of direction - looking for examples (Part XXV) |
The ”curves of direction” go back to G. Salmon and E. Laguerre who gave their name to these curves which have a link with caustics by reflection and interesting properties. Curves of direction are caustics for parallele light rays with the condition to be algebraic and to have an algebraic expression of the element of arc. |
A selection of special plane curves Ck(n, p) and a few properties - Cyclodes. (Part XXVI) |
We have selected some plane curves in the series of generalized sinusoidal spirals called Ck(n, p). And give various properties using elementary geometry or analytic transformations like Gregory’s and Mc Laurin’s, pedals, evolutes and involutes. One section is devoted to the Cyclodes of Sylvester. |
|
Rectangular hyperbola - circle geometric properties and formal analogies (Part XXIII) |
We review some selected elementary properties of the rectangular hyperbola and compare to those of the circle. The rectangular hyperbola has great analogy and many corresponding characteristics. An important application is the analogic definition of hyperbolic trigonometry on the model of circular trigonometry and circular functions. |
Biangular and bipolar coordinates defining plane curves Sectrices of Maclaurin / Plateau's curves (Part XXIV) |
Some curves have a simple definition in a biangular system of coordinates. A point A in the plane is located by a system of two lines rotating around two fixed points B, C on an xx'-axis and two angles (θ, θ'). Triangle ABC defines a biangular coordinate system if the two angles depends on one parameter. A similar system is the bipolar coordinates (well known for central conics and their foci), with distances (ρ, ρ') to the poles (B, C) fixed on axis-x'x and a relation between the two lengths. We examine a few examples of the Maclaurin sectrices or Plateau’s curves. |
|
Curves of direction, minimal surfaces and conjugate perpendicular geodesic duality (Part XXI) |
We explore some links between Laguerre curves of direction (COD), Minimal sufaces (MS) and conjugate perpendicular geodesics (CPG). MS are considered as analytic extensions in 3rd dimension of the two dimensional COD. |
Equality of arc length of the parabola and the Archimede spiral. (Part XXII) |
We go through a short period of history of the beginning calculus (1643-1668) when two classical curves : the parabola and the Archimede spiral were implicated and contributed to progress in understanding the new calculus. |
|
TANGENTIAL GENERATION CURVES AS ENVELOPES OF LINES OR CIRCLES. ARCUIDS AND
CAUSTICOIDS (Part XIX) |
We present a tangential approach to the definition of plane curves. The ponctual definition is most used because the point P(x, y) is a precise object unlike the tangential definition since the point of contact of the line with its envelope is not given. We propose the tangential definition as a natural method. |
Tangential dual of Steiner-Habich Theorem, circular tractrices, newtonian catenaries, circles
as roulettes of a curve on a line (Part XX) |
We present a dual of Steiner-Habich theorem : tangential generation of curves as envelope of a line attached to a curve rolling on a line. We apply this to the study of circular tractrix, its evolute and the pedal of this evolute. This gives a simple method to generate tangentially the circle as the roulette of a plane curve (a newtonian catenary) on a line. |
|
Cesaro’s curves : A generalization of cycloidals (Part XVII) |
In the years 1886-1900 E. Cesaro published in Mathesis and the Nouvelles Annales de Mathematiques several papers about a large class of curves with interesting properties. These are expansion of a special property of conics and cycloidals. Later he studied a class defined by an intrinsic equation with two parameters λ and μ and a length R as subclasses of his curves. After a short story of the Cesaro curves, we present a generalization of the cycloidals using Mc Laurin and pedal transformations. |
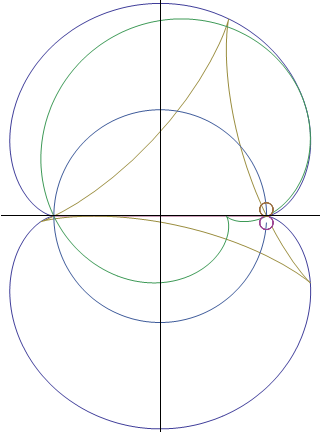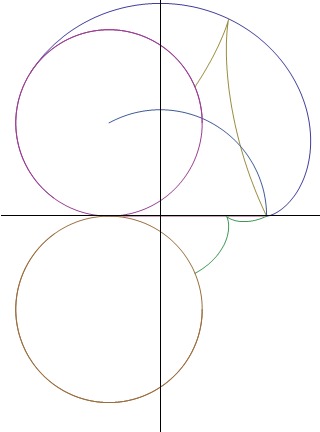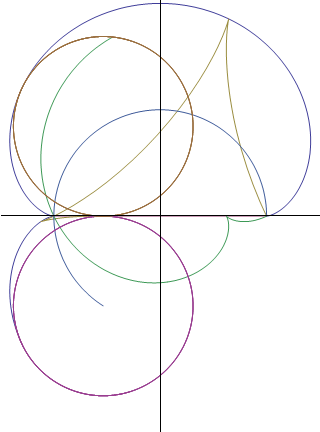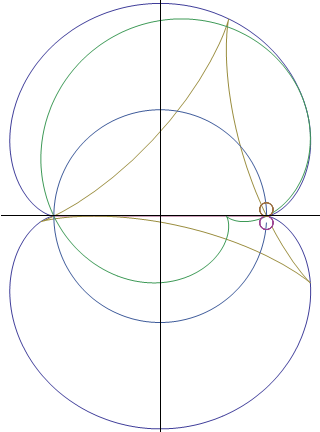
Astroid - Nephroid, Deltoid - Cardioid, Orthocycloidals (Part XVIII) |
We present a transformation that links couples of orthocycloidals and curves transformed by central inversion. We apply it to astroid/nephroid and deltoid/cardioid and give a proof of an old central polar equation of the Nephroid. |
|
Rational expressions of arc length of plane curves by tangent of multiple arc and curves of
direction. (Part XV) |
We present some examples of parametrized plane curves which have a computable arc length in the context of integration in finite terms, by elementary algebraic expressions and their logarithms. We examine polynomials and rational arc lengths which are an important classes of curves useful in CAGD and PH-curves. |
Logarithmic spiral, aberrancy of plane curves and conics. (Part XVI) |
A local property of a plane curve is examined as a generalization of approximation of a curve by its tangent line or its osculating circle (the curvature) which is symetrical w.r.t. the normal. The aberrancy is a local parameter measuring the shift from this symmetry. Abel Transon in his 1841 paper write "define the aberrancy by mean of the osculating logarithmic spiral could not present any difficulty" but used conics instead of the logarihmic spiral which however gives a simpler purely geometric concept of a "deviation". |
|
Catacaustics, caustics, curves of direction and orthogonal tangent transformation. (Part XIII) |
We give some properties of a tangential axial transformation used by d'Ocagne and Cesaro and others : the orthogonal tangents Transformation (OTT) and present two associated transformations bisector and anti-bisector. These are simple tools to study caustics by reflection for parallele rays of light and curves of direction. |
Variable rolling circles, orthogonal cycloidal trajectories, envelopes of variable
circles. (Part XIV) |
We recall some properties of cycloidal curves well known for being defined as roulettes of circles of fixed radius and present a generation using using variable circles as a generalisation of traditional roulettes so to bring some different approach of these curves. We present two types of associated epi- and hypo-cycloids that have orthogonality properties and give a new point of view at classical examples. We describe how two associated cycloidal so that they can rotate inside a couple of cycloidal envelopes and stay constantly crossing with a right angle. |
|
Inversion, Laguerre T.S.D.R., Euler polar tangential equation and d'Ocagne axial
coordinates. (Part XI) |
We present a natural correlative of the inversion (transformation by reciproqual radii) in 2-dimensional euclidean space : the Transformation par Semi Droites Reciproques proposed by E. Laguerre about 1880 and give some elementary properties. This TSDR is a tangential version of the inversion and shares with it many correlative characteristics. Two systems of coordinates in the plane are described : polar tangential coordinates which goes back to Euler and axial coordinates (λ,θ) exposed by M.d'Ocagne (1884). We give examples of tangential axial transformations. |
Caustics by reflection, Curves of direction, Rational arc length. (Part XII) |
Caustics by reflection and curves of direction have, when algebraic as shown by E.Laguerre and G.Humbert, a rational arc length. Examples of low order caustics are drawn with help of geometric definition of catacaustics. For conics the caustic is in general of order 6. We present links with classes of curves of direction studied by Cesaro, Balitrand and Goormaghtigh in NAM between 1885 and 1920. |
|
DUPORCQ CURVES, STURMIAN SPIRALS, ROULETTES AND
GLISSETTES (Part IX) |
We present some properties of the Duporcq curves and Sturmian spirals from the point of view of Gregory's transformation. These two classes of plane curves are related to the conics and present interesting associated particularities. We use eccentricity e of conics as the parameter of form for the two classes (Duporcq and Sturm). |
INTRINSICALLY DEFINED PLANE CURVES, CLOSED OR PERIODIC CURVES AND GREGORY’S
TRANSFORMATION (Part X) |
Cesaro defined plane curves by its intrinsic equation : a relation between the radius of
curvature (Rc) and the arc length s counted from a fixed point on the curve. We give
some examples. |
|
Gregory's transformation (part I) |
James Gregory in his book "Geometria pars universalis -1668" presented a general transformation in the plane which associates a curve in polar coordinates (ρ,θ) to a curve in cartesian orthonormal coordinates (x,y). We examine geometric properties of these corresponding couples of plane curves and use the terms ground (x,y) and wheel (ρ,θ) to name the couple of associated objects defined by Gregory's transformation. |
Euler Serret curves (wheels for a circle ground - part II) |
We use the Gregory's transformation to study a problem from Euler: to find algebraic curves with the same arc length as the circle. Serret, in the middle of 19th century found, using an algebraic calculation, an infinite serie of algebraic curves. Gregory's formulas give a solution and a geometric interpretation of the results of Euler and Serret. This could be used to find curves with same arc length as the ellipse or the lemniscate. |
|
A generalization of Ribaucour curves and sinusoidal spirals (part III) |
We use two transformations Mc Laurin and pedal to define classes of plane curves that generalise the sinusoidal spirals. Since these spirals are wheels for the curves of Ribaucour, the properties of the couple wheelground associated by the Gregory's transformation in polar coordinates and in cartesian orthonormal coordinates give a simple generalisation. The common parameter of all curves is the angle V=(ray-tangent) or a multiple of this angle. |
Tschirnhausen's Cubic (Part IV) |
We present some properties of the Tschirnhausen's Cubic related to the couples ground-wheel and gregory's transformation. |
|
Closed wheels and Periodic grounds (Part V) |
The property of Cardan-Al Tusi is the generic example of a couple wheel-ground as defined by the Gregory's Transformation. We study some characteristics of the couple wheel-ground for which the wheel and the corresponding ground are closed or periodic curves. We explore some examples to illustrate the topic just a glance through the subject. | Catalan's wheel (Part VI) | We use theorems on roulettes and Gregory's transformation to study Catalan's curve in the class C2 (n; p) with angle V = π/2 - 2u and curves related to the circle and the catenary. Catalan's curve is defined in a 1856 paper of E. Catalan "Note sur la theorie des roulettes" and gives examples of couples of curves wheel and ground. |
| Anallagmatic Spirals-Pursuit Curves-Hyperbolic-Tangentoid Spirals-Beta Curves (Part VII) | By analogy with sinusoidal spirals and Ribaucour curves defined with trigonometric functions we use Mc Laurin and pedal transformations to study classes of plane curves : tangentoid and anallagmatic spirals defined with hyperbolic functions and gudermanian. We examine the grounds associated to these curves as wheels by the Gregory´s transformation and orthogonal trajectories and describe some special families of curves depending of two integer indexes. | Translations-Rotations-Orthogonal Trajectories-Gregory's Transformation (Part - VIII) | With help of Gregory's Transformation and two plane isometries : translations and rotations we examine the orthogonal trajectories of curves with parameters xo and θo and give some properties of families of curves associated by the GT. By analogy with the families of sinusoidal spirals and Ribaucour curves we present families of curves depending of Mc Laurin index n. |
